Числовые тесты на проценты

Оценка персонала и кандидатов при приеме на работу практически всегда включает в себя числовые тесты. А понятие процента используется очень широко в числовых тестах при приеме на работу. Это задания на расчет прибыли и убытка, соотношений, пропорций, теории чисел и интерпретации данных. Кроме того, существует отдельный раздел тестов, где проценты считается важнейшей составляющей.

Задачи на расчет процентов входят в обязательный набор числовых тестов в консалтинговые и аудиторские компании, банки, страховые компании и бухгалтерские отделы практически всех крупных организаций. Тесты Лидеры России и других кадровых конкурсов используют числовые тесты на проценты в обязательным порядке. Если вам предстоит проходить числовые тесты, то мы рекомендуем отработать задачи на проценты в первую очередь.

Понятие процента и процентного соотношения

Процент представляет собой число или отношение, выраженное в виде доли от 100. Таким образом, 20% означает 20/100. Процент является одним из самых простых инструментов для сравнения данных, так как помогает сравнивать различные дроби, особенно в случаях дробей с различными знаменателями.

Под процентом мы подразумеваем, что это сотые доли от целого. Таким образом, х процентов означает х сотых, записанных как х%.

Чтобы выразить x% как дробь, мы имеем x% = x / 100.

Таким образом, 20% = 20/100 = 1/5.

Чтобы выразить a / b в процентах, мы имеем, a / b = (a / b) * 100%.

Таким образом, 1/4 = (1/4) * 100% = 25%.

Способы подсчета задач на проценты

1. Если A на R% больше, чем B, то B меньше, чем A на R / (100 + R) * 100
2. Если A на R% меньше, чем B, то B больше, чем A на R / (100- R) * 100
3. Если цена товара увеличивается на R%, то: R / (100 + R) * 100
4. Если цена товара уменьшается на R%, то: р / (100-р) * 100

Расчеты роста или снижения населения

Пусть население города сейчас будет P и предположим, что оно увеличивается со скоростью R% в год;

1. Население после n лет = P (1+ (R / 100))
2. Население n лет назад = P / (1+ (R / 100))
3. Если население увеличивается на x% в течение первого года, на y% в течение второго года, на z% в течение третьего года, население через три года будет:

P (1 + x / 100) ( 1 + у / 100) (1 + Z / 100)

Прогрессия в тестах на проценты

1. Если число увеличивается на х%, а затем уменьшается на х%, то число будет уменьшено на х²/100 процентов
2. Если число уменьшается на х%, и затем увеличилось на х% , то число будет уменьшено на х²/100 процентов
3. Если на экзамене, в котором минимальный процент прохождения составляет x%, кандидат получает оценку y и падает на z баллов, то общее количество баллов в этом экзамене будет 100 * (y + z) / x
4. Если на экзамене x% и y% кандидатов соответственно, потерпели неудачу в двух разных предметах, а z% кандидатов не сдавали оба предмета, то процент кандидатов, сдавших оба предмета, будет равен [100- (x + y + z). )]%

Расчеты цен, прибыли или убытка

1. Если цена продукта увеличивается или уменьшается на x%, а другой фактор уменьшается на y%, то результат определяется как:

[x + y + xy / 100]%

2. Если результат равен нулю, т. е. нет ни потерь ни прибыли, тогда приведенная выше формула имеет вид:

y = 100x / 100 + x

3. Если цена товара последовательно увеличивается на x%, y% и z%, то конечное увеличение цены составит:

[x + y + z + {xy + yz + zx} / (100) + xyz / 100²]%

4. Если после расходования сначала p1%, затем p2% от остатка и т. д., B — это сумма баланса, то общая (исходная) сумма определяется как:

Общая сумма = B * 100 * 100 ….. / (100-р2) …..

Читайте нашу отдельную статью Числовые тесты на расчет прибыли и убытка

Таблица основных показателей процентных величин

Если вы готовитесь к числовым тестам на проценты или доли, мы настоятельно рекомендуем потратить несколько часов и выучить данную таблицу. Это поможет сэкономить вам драгоценное время по время прохождения реального тестирования.

Доля	Десятичный	Процент
1/2	0,5	50%
1/3	0,333	33,333%
2/3	0,666	66,666%
1/4	0,25	25%
3/4	0,75	75%
1/5	0.2	20%
2/5	0,4	40%
3/5	0.6	60%
4/5	0.8	80%
1/6	0,1666	16,666%
5/6	0,8333	83,333%
1/8	0,125	12,5%
3/8	0,375	37,5%
5/8	0,625	62,5%
7/8	0,875	87,5%
1/9	0,111	11,111%
2/9	0,222	22,222%
4/9	0,444	44,444%
5/9	0,555	55,555%
7/9	0,777	77,777%
8/9	0,888	88,888%
1/10	0,1	10%
1/12	0,08333	8,333%
1/16	0,0625	6,25%
1/32	0,03125	3,125%

Примеры числовых тестов и задач на проценты

Для успешного решения задач на числовом тестировании кандидаты должны уметь решать разнообразные задачи на проценты. Ниже мы приведем большой набор тестов на проценты с ответами и объяснением для вашей самостоятельной практики.

1. Какой процент составляет 2 минуты 24 секунды от 1 часа?

• а. 6%
• b. 2%
• с. 4%
• d. 8%

2мин 24 с = 144 с

144 * 100/60 * 60 = 4%

2. Добавление 20% от x к x эквивалентно умножению x на какое из следующих чисел?

• a. 12,5
• b. 1,05
• с. 1,15
• d. 1,20

120x/100 = 1,2 * x

3. Каково значение 8¹/₃% от 600+ 37^½% от 400

• а. 100
• b. 300
• с. 150
• d. 200

25 * 600/300 + 75 * 400/200 = 50 + 150 = 200  — ну да 8¹/₃% =25/300 и 37^½%=75/200, т.е. здесь процент представляется удобной дробью

4. Две трети из трех пятых из пяти шестых числа — это какой процент от этого числа?

• а. 66²/₃%
• b. 33¹_/3%
• с. 60%
• d. 40%

2/3 * 3/5 * 5/6 = 1/3

1/3 х/х * 100 = 100/3 = 33¹_/3%

5. Из-за сокращений персонала производство на фабрике уменьшилось на 40%. На сколько процентов следует увеличить рабочее время, чтобы восстановить первоначальный уровень производства?

• а. ₆₆²_/3%
• b. 46¹_/3%
• с. 25%
• d. 40%

Увеличение рабочего времени: 40*100/(100-40) = 4000/60 = 66²/₃%

6. Заработная плата всех сотрудников увеличилась дважды последовательно на 20%. Каков общий процентный рост их зарплат?

• а. 20%
• b. 40%
• с. 21%
• d. 44%

Коэффициент изменения (КИ) = 120/100 * 120/100 = 36/25

Общий % увеличения = (КИ — 1) * 100 = (36/25-1) * 100

Или 11/25 * 100 = 44

7. На экзамене кандидату необходимо набрать 45% от максимально возможной оценки. Кандидату, получившему 180 баллов, не хватило для прохождения 45 баллов. Найдите значение максимально возможной оценки.

• а. 450
• b. 600
• с. 500
• d. 550

Обозначим максимально возможную оценку через х,

Тогда проходной балл будет = 45x/100

По условию задачи: 180 = 45x/100-45

х = 180 * 100-4500 / 45 = 500

8. К 50 литрам раствора, содержащего 20% спирта в воде, добавили еще 10 литров воды. Какова крепость полученного раствора?

• а. 20%
• b. 16²_/3%
• с. 12¹/₂%
• d. 33 1/₃%

Количество спирта в 50 литров = 50 * 20/100 = 10

Таким образом, крепость (% спирта) в 60 л раствора = 10/60 * 100 = 100/6 = 16²_/3

9. Население города увеличивается ежегодно на 20%. Если начальное население составляло 2 000 000, то какова разница прироста населении через два и три года?

• а. 632500
• b. 488000
• с. 608000
• d. 576000

Коэффициент прироста численности населения через 2 года = 120/100 * 120/100 = 36/25

Коэффициент прироста численности населения через 3 года = 120/100 * 120/100 * 120/100 = 6/5 * 6/5 * 6/5 = 216/125

Прирост через 2 года = 2000000 * 36/25 = 2880000

Прирост через 3 года = 2 000 000 * 216/125 = 3456000

Разница = 3456000 — 2880000 = 576000

10. Население города уменьшилось на 10% в конце первого года и увеличилось на 10% в конце второго года, и снова уменьшилось на 10% в конце третьего года. Если население города на конец третьего года составило 4455 человек, то каково было население города на начало первого года?

• а. 5000
• b. 4500
• с. 4950
• d. 1000

Коэфф-т изменения (КИ) = 90/100 * 110 * 100 * 90/100 = 81 * 11/1000

Население на начало 1 года = 4455/КИ = 4455 * 1000/81 * 11 = 5000

11. При снижении цены товара на 11¹/₉%, продажи увеличились на 12^1/2%. Как это повлияло на доходность?

• а. Убыток 1%
• b. 1% прирост
• с. Нет убытка и нет прибыли
• d. Не может быть определено

Коэфф-т снижения цены = (100-100/9)/100 = 800/900 = 8/9

КИ увеличения продаж = (100 + 25/2)/100 = 225/200 = 9/8

Сам поставил в этих выражениях скобки — может и не надо, мозг закипает как это получается чисто математически, пусть Ирина посмотрит

Общий КИ = 8/9 * 9/8 = 1

Общий % изменения (изменение доходности) =

(Общий КИ — 1) * 100 = (1 — 1) * 100 = 0

12. Экзамен успешно сдали 80% мальчиков и 40% девочек. Девочек, которые сдали экзамен – 120, и это 2/3 от числа мальчиков, которым это не удалось. Каково общее количество школьников, которые пришли на экзамен?

• а. 1200
• b. 380
• с. 3800
• d. 2180

Пусть количество мальчиков — x, количество девочек – y.

40y/100 = 120

у = 300

120 = 2/3 * 20x/100 = 2x/15

х = 900

Всего = х + у = 300 + 900 = 1200

13. Население городов А и Б одинаково. Население города А увеличивается в течение двух лет последовательно на 20% и 15% в год, а население города Б – аналогично, на 20% и 10%. Если разница в населении двух городов через 2 года составляет 768 человек, то какова была общая численность населения этих двух городов изначально?

• а. 12800
• b. 26500
• с. 24600
• d. 25600

Население города А = население города Б = А

Коэфф-т изменения (КИ) по A = 120/100 * 115/100 = 138/100

КИ по B = 120/100 * 110/100 = 132/100

Население А через 2 года = А * 138/100

Население B через 2 года = A * 132/100

Разница = A / 100 (138–132) = 768

A = 768 * 100/6 = 12800

Общая начальная численность населения = 12800 + 12800 = 25600

14. Какое количество воды следует добавить, чтобы уменьшить концентрацию 5 литров 45%-й кислоты до 25%?

• а. 3 литра
• b. 2 литра
• с. 4 литра
• d. 5 литров

Количество кислоты в 5 л = 45 * 5/100 = 2,25 л

Пусть к раствору добавили X литров воды, тогда в (5+ X) литров жидкости находится 2,25 литра кислоты.

25% (5 + X) = 2,25 или  25/100*(5 + X) = 2,25

Х = (225-125)/25 = 4

15. A, B и C участвуют в выборах в определенном округе. A и B вместе получили на 50% больше голосов, чем получил C. Совместная доля голосов A и C на 30 процентных пунктов больше, чем доля B. Кто победил на выборах?

• а. А
• b. В
• с. С
• d. Не может быть определено

Пусть a, b, c — доли голосов A, B, C соответственно

а + b = 1,5 с

а + с = b + 30

a + b + c = 100, 2b + 30 = 100,

b = 35

а = 25, с = 40, итак, С победил на выборах.

16. На экзамене Дмитрий получил на 8% меньше проходного балла, а Михаил получил на 20% больше проходного балла. Если разница между процентами от их оценок составляет 14, то каков проходной процент?

• а. 40%
• b. 50%
• с. 60%
• d. не может быть определено.

Пусть P будет проходной процент, тогда

Дмитрий получил 0,92%, а Михаил получил 1,2%

По условию задачи 1,2 P — 0,92 P = 14

P = 14 / 0,28 = 50%

17. Зарплаты A и B в сумме 14000 рублей. А тратит 80% своей зарплаты, а В — 85% своей зарплаты. Какова зарплата B, если их остатки от зарплаты одинаковы?

• а. 6000 рублей
• b. 8000 рублей
• с. 7500 рублей
• d. 6500 рублей

Пусть зарплаты A и B равны X и Y соответственно

X + Y = 14000

Остаток A = 20X/100 = Остаток B = 15Y / 100

X = ¾ Y

3/4Y + Y = 14 000, 7 Y/4 = 14 000, Y = 8000

18. Сумма в 395 рублей была разделена между A, B и C таким образом, что B получил на 25% больше, чем A и на 20% больше, чем C. Какова доля A?

• а. 195 рублей
• b. 180 рублей
• с. 98 рублей
• d. 120 рублей

Пусть доля каждого будет A, B и C соответственно, тогда

B = 125A/100 = 120C / 100

A = 100B/125 = 4/5B, C = 100B/120 = 5/6B

4/5B + B + 5/6B = 395, 79B/30 = 395, B = 395 * 30/79 = 150

A = 4 * 150/5 = 120

19. Есть три положительных целых числа, так что 70% первого числа, 58¹/₃% второго числа и 38⁸/₉% третьего числа равны. Какие из следующих чисел являются этими тремя числами?

• а. 5,6,9
• b.10,12,18
• c.15,18,27
• d.Все три числа одинаковы

Все три доли находятся в одинаковом соотношении

20. Есть два числа. Утроенное первое число на 20% больше, чем удвоенное второе, если второе увеличить на 105. Если к удвоенному первому числу прибавить 36, то это будет на 20% меньше, чем утроенное второе число. Определите значение первого числа.

• а.150
• b.162
• с.180
• Ни один из них

Пусть первое число будет х, второе — у.

3x = 1,2 (2у + 105)

3x = 2,4 у +126 ……………… .. (1)

2x + 36 = 0,8 (3 у)

2x +36 = 2,4 у ……………… .. (2)

х = 162

У большинства работодателей применяются числовые тесты от разработчиков SHL, Talent Q, Kenexa, Saville и других разработчиков. В тестах на проценты этих компаний данные всегда представлены в виде таблиц, графиков или диаграмм. Приведем пример числового теста на проценты от CEB SHL.

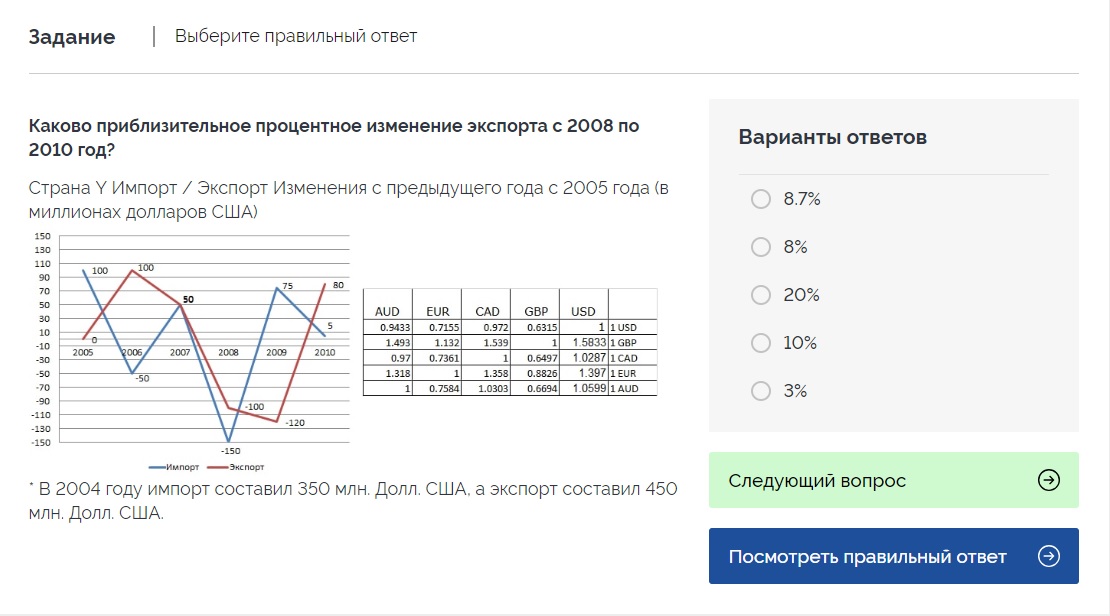
Ответ:

Финансовые тесты на проценты для самостоятельных расчетов

Продавец получил прибыль, равную продажной цене 75 изделий, когда продал 100 изделий. Какую прибыль он получил от сделки?

• A) 33,33%
• B) 75%
• C) 300%
• D) 150%

Торговец покупает две партии товара за 600 рублей. Он продает одну из них с прибылью 22%, а другую — с убытком в 8% и в итоге не теряет прибыли. Какова цена продажи товара, который продается с убытком?

• А) 404.80 рублей
• В) 440 рублей
• С) 536,80 рублей
• D) 160 рублей

Продавец заявил, что продает свой товар с потерей в 8%, но весит он 900 граммов вместо веса в килограмм. Найдите его реальную потерю или прибыль.

1. A) 2% потерь
2. B) 2,22% прибыли
3. C) 2% прибыли
4. D) Ничего из этого

Роман продал товар за 56 рублей, а себестоимость товара Х рублей. Если он получил х% от своих расходов, какова была себестоимость?

• А) 40 рублей
• B) 45 рублей
• C) 36 рублей
• D) 28 рублей

Магазин покупает товар по сумме 19% от цены на этикетке. Если он хочет получить прибыль в размере 20% после предоставления суммы в 10%, на какой процент его цена должна превышать первоначальную цену на этикетке?

• A) + 8%
• B) -3,8%
• C) + 33,33%
• D) Ни один из них

Если яблоки покупаются из расчета 30 штук за рубль, то сколько яблок нужно продавать за рубль, чтобы получить 20% прибыли?

• A) 28
• B) 25
• C) 20
• D) 22

Два торговца продают каждый предмет за 1000 рублей. Если торговец A рассчитывает свою прибыль по себестоимости, а торговец B вычисляет свою прибыль по продажной цене, они получают прибыль в размере 25% соответственно. Насколько прибыль, полученная Торговцем B, больше, чем прибыль Торговца A?

• A) 66,67 рублей
• B) 50 рублей
• C) 125 рублей
• D) 200 рублей

Продавец продает свои товары таким образом, чтобы прибыль от продажи 50 товаров равнялась продажной цене 25 товаров. Какова его прибыль?

• A) 25%
• B) 50%
• C) 100%
• D) 66,67%

Торговец продает свой товар на 75% выше его себестоимости. Какую максимальную сумму в процентах он может предложить, чтобы он в конечном итоге продал без прибыли или убытка?

• A) 75%
• B) 46,67%
• C) 300%
• D) 42,85%

Ключи к ответам:

1.C;  2.A;  3.B;  4.A;  5.A;  6.B;  7.B;  7.B;  8.C;  9.D

---

Числовые тесты на проценты могут быть очень непростыми. Основная их сложность заключается даже не в самих расчетах, а в том, что их требуется решить за ограниченное время — обычно 60 секунд. Но нет ничего невозможного. За 3-4 дня практики на HRLider.ru вы увидите разные примеры числовых тестов и поймете, как их решать быстро и точно. Если вам предстоят числовые тесты, подготовьтесь — гарантируйте свой успех.

Начните с того, чтобы посмотрите наши тесты бесплатно в режиме демо-доступа по кнопке Попробовать бесплатно.

Попробовать бесплатно

Начать подготовку

Если вы представитель работодателя, то с нами вы сможете провести оценку компетенций и интеллектуальных способностей кандидатов.  Платформа тестирования персонала EMPLOYER.HRLIDER создана, чтобы помочь вам проводить эффективную и быструю оценку персонала и кандидатов на работу в вашу компанию. Наши преимущества – простота использования, доступность (средняя стоимость одного тестирования – 80 рублей) и надежность результатов.

Наши клиенты сообщают, что качество найма (удержание и производительность) у новых сотрудников выросло на 45-50%, а затраты времени и сил на подбор и оценку персонала сократились до 60%.

Позвоните нам для консультации по телефону или в мессенджерах +7906-13-77-333 и начните работу на EMPLOYER.HRLIDER за 10 минут!

---

Читайте больше о числовых тестах и методиках их быстрого решения в наших статьях:

Числовые тесты при приеме на работу, что это, примеры с ответами, советы как решать